常见的路由协议比如RIP、IGRP、BGP是距离矢量协议，OSPF和ISIS是数据链路状态协议。矢量协议路由器只知道本身和与自身相连的接口路由信息，矢量图只是一张方向图，在路由传播的过程中，容易造成环路。RIP路由器采用扁平化设计规避环路，BGP则采用As-path规避环路。OSPF是数据链路状态路由协议，采用的SPF算法，即最小生成树算法（Dijkstar），ospf内不存在路由环路，但是OSPF间传递路由信息的时候，却是矢量路由协议，也就是说OSPF之间传递路由信息的时候，会产生路由环路。

       Dijkstar 算法：

   1、 算法目的：

    在无向图 G=(V,E) 中，假设每条边 E[i] 的长度为 w[i]，找到由顶点 V0 到其余各点的最短路径。（单源最短路径）

   2、 算法描述：

    算法思想：设G=(V,E)是一个带权有向图，把图中顶点集合V分成两组，第一组为已求出最短路径的顶点集合（用S表示，初始时S中只有一个源点，以后每求得一条最短路径 , 就将加入到集合S中，直到全部顶点都加入到S中，算法就结束了），第二组为其余未确定最短路径的顶点集合（用U表示），按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中，总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外，每个顶点对应一个距离，S中的顶点的距离就是从v到此顶点的最短路径长度，U中的顶点的距离，是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。

   3、算法步骤：

a.初始时，S只包含源点，即S＝{v}，v的距离为0。U包含除v外的其他顶点，即:U={其余顶点}，若v与U中顶点u有边，则<u,v>正常有权值，若u不是v的出边邻接点，则<u,v>权值为∞。

b.从U中选取一个距离v最小的顶点k，把k，加入S中（该选定的距离就是v到k的最短路径长度）。

c.以k为新考虑的中间点，修改U中各顶点的距离；若从源点v到顶点u的距离（经过顶点k）比原来距离（不经过顶点k）短，则修改顶点u的距离值，修改后的距离值的顶点k的距离加上边上的权。

d.重复步骤b和c直到所有顶点都包含在S中。

    4、算法实例：

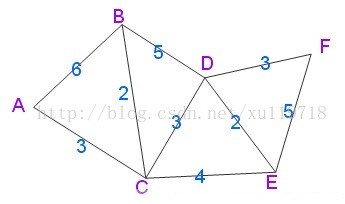
用算法找出以A为起点的单源最短路径步骤如下

即已A为根节点，对树进行遍历的结果：s=<A、C、B、D、E、F>